용역기간 : 2000년 6월 1일 ~ 2000년10월 20일
검증법: 전기회로 계의 미분방정식과 수치 해
발주자: (주)에너지 앤 그라운드 뱅크(현, (주) 그라운드)
(주)신세기통신
시행자: 선문대학교 이학박사 안승준 교수 ( 신소재과학과 )
선문대학교 이학박사 박철근 교수 ( 전자정보통신공학부 )
선문대학교 이학박사 안성준 교수 ( 전자정보통신공학부 )
전기회로계의 미분방정 식과 수치해
◎전기회로계

계의 동적 거동은 중요한 관심의 대상이다. 역학적 계는 이동거리, 속도, 그리고 가속도 등을 포함하고 있다. 전기 또는 전자계는 전압, 전류 그리고 이들의 시간 함수를 포함한다. 일반적으로, 동적 성질을 묘사하기 위해 사용되는 방정식들은 이동거리, 전류와 그들의 미분 항들을 미지변수로 포함하고 있다. 미지함수 의 1계 또는 그 이상의 상미분항을 포함하고 있는 방정식은 상미분 방정식이라 불리고 약어로 상미방(ODE: Ordinary Differential Equation)으로 불리기도 한다. 방정식 의 계수(order)는 최고차의 도함수의 계수에 의하여 결정된다. 예를 들어, 만일 1계 도함수가 유일한 미분항이면 그 방정식은 1계 상미방이 된다. 한편, 최고차의 도함 수가 2계이면 그 방정식은 2계 상미방이라 불리운다. 이렇게 하여 전기 회로계는 보통 2계 상미방으로 표현되는데, 그림에 보이는 회로의 전류는 다음 적분-미분방정식 의 지배를 받는다.
 (1) (1)
 (2) (2)
여기서 q(t)는 축전기 전하(coulomb)이다. 스위치는 t=0에서 폐쇄되어 있다고 가정하고 i=i(t)는 전류 그리고 상수들은 다음과 같이 결정된다.
R = 100~10 (100, 50, 20, 10)Ω;
L = 1.0e-8, 1.0e-7, 1.0e-6 H;
C = 1.0e-8, 1.0e-7, 1.0e-6 F;
E(t) = δ(t) : impulse function;
초기 조건들은 q(0)=0 (축전기의 초기 전하) 이고 i(o)=0 이다.
☞식 (2)를 미분하면 다음과 같다.
 (3) (3)
☞식 (1)을 다시 쓰면 다음과 같다.
 (4) (4)
◎상미분방정식(4)의 수치해
상미방을 풀기 위한 문제들은, 주어진 영역의 경계점에서 조건들이 어떻게 표시되는가에 따라 초기치 문제 또는 경계치 문제로 구분되어 진다. 초기치 문제의 모든 조건들은 영역의 시작점에서 표시된다. 반대로 조건들이 영역의 시작점과 종결점으로 나누어서 정 의되면 이 문제는 경계치 문제가 된다. 일반적으로 시간영역에서의 상미방은 초기치 문제이며, 따라서 모든 조건들은 초기 시간인 t=0에서 주어진다. 그러므로 여기서 우리가 고려하는 전기회로계는 2계 상미방의 초기치 문제로귀착된다.
○Euler 방법
상미방에서 최고계의 도함수가 2계 도함수일 때, 이 상미방은 2계 상미방이라 불리운다. 2계 상미방은 다음과 같이 주어진다[ 식 (4) 참조]. < P>
 (5) (5)
여기서 a, b와 s는 상수 또는 t, u와 u의 함수이다. 그리고 두 번째와 세 번째의 식들은 초기 조건이 된다. 2계 상미방은 2게의 초기 조건들을 필요로 하며, 이는 u(0)와 u(0)로 주어져 있다. 만약 a, b와 s가 u에 무관하다면, 위 식은 선형 상미방이 된다. 이렇게 하여 전기회로계 상미방은 2계 선형 상미방이 된다. 여 기서는 전방 Euler 법에 의한 2차 상미분 방정식을 MATLAB을 이용하여 수치적으로 계산하는 방법을 간단히 소개하고 해당 프로그램을 제공한다. 4차 Runge-Kutta 법을 적용하여 MATLAB로 수치해를 얻는 보다 정확한 방법은 다음절에서 소개하며, 본 연구에서는 이 4차 Runge- Kutta 법으로 미분방정식의 초기치 문제를 해결하기로 한 다.
Euler 법을 적용하기 전의 중요한 단계는 2차 상미방을 1계 상미방의 쌍으로 나누는 것이다. 다음과 같이 정의하자.

그리고나면, 식(7)은 다음과 같이 표현 된다.

여기서 새로운 변수인 v의 항으로 나타내어야 하는 초기조건은 식 (5)의 2번째 초기조건으로부터 도출된다. 식 (5)는 이제 동치인 다음과 같은 연립 1 계 상미방으로 나타난다.
 (6) (6)
여기서

MATLAB을 적용하기 위하여, 각 시간단계 동안의 계산은 행렬의 형태로 쓰여질 수 있다. 우선 y와 f를 다음과 같이 정의하자.
 (7) (7)
그러면 방정식 (6)은 다음과 같은 단일 방정식으로 쓰여진다.

위 식에 의해 전방차분 근사를 사용하는 Euler 식은 다음과 같이 주어진다.
 (8) (8)
☞우리가 해결해야 할 식 (4)에 대한 식 (8)의 Euler 알고리즘을 얻기 위해 벡터형으로 표현하면 다음과 같다.
 (9) (9)
여기서
 (10) (10)
☞식 (8), (9), (10)을 이용하여 MATLAB 스크립트를 작성하면, 다음과 같은 프로그램을 얻는다.

○4차 Runge-Kutta 방법
Euler 법의 주요한 결점은 정확도가 낮다는 것이다. 높은 정확도를 얻기 위해서는 식 (8)에 나타나는 h가 작은 값이어야 하는데, 이로 인하여 계산 소 요시간이 길어지고 무시 못할 반올림오차를 유발하기도 한다. Runge- Kutta 방법은 Euler 법의 이러한 부정적인 면을 개선하며 h가 감소함에 따라 오차가 더욱 빨리 감 소하게되는 장점을 가지고 있다.
다음의 상미방을 고려하자
 (11) (11)
알고 있는 yn의 값에 대하여 yn+1를 계산하기 위해, 의 구간에서 위 식을 적분하면 다음과 같다.
 (12) (12)
위 식 (12)의 적분의 근사값을 구하기 위해, 2차 Runge-Kutta법은 사다리꼴 공식을 이용하며, 3차 Runge-Kutta법은 심프슨(Simpson)의 1/3 법칙을 이 용한다. 4차 Runge-Kutta법은 심프슨(Simpson)의 1/3 법칙 혹은 3/8 법칙에 기초하며, 테일러(Taylor) 전개의 4차항 만큼 정확하기 때문에, 국지적 오차는 h5에 비례한다. 한편, 심프슨 1/3법칙에 기초한 Ringe-Kutta 법의 알고리즘은 다음과 같이 주어진다.
 (13) (13)
☞우리가 관심을 가진 식 (6)의 두 방정식 집합에 대하여 4차 Runge-Kutta 법을 적용하면 다음과 같은 식을 얻는다.
 (13) (13)
위 식을 벡터형으로 나타내면 다음과 같다.
 (14) (14)
이로부터 4차 Runge-Kutta 법은 다음과 같이 주어진다.
 (15) (15)
☞4차 Runge-Kutta 법을 구현하기 위한 MATLAB 스크립트(프로그램 파일)는 위 식을 사용하여 작성 가능하다. 식 (6)과 함께, 위 식을 행렬(matrix) 형 으로 나타내면 다음과 같다.

 (16) (16)
그리고
 (17) (17)
☞우리가 해결해야할 식 (4)에 4차 Runge-Kutta법을 적용한 MATLAB을 위한 알고리즘을 구현하자. 식 (16)으로부터 다음식을 얻는다.


그리고 식 (17)으로부터 다음 알고리즘을 얻는다.
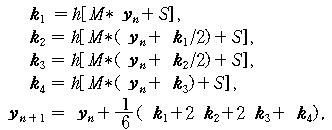 (18) (18)
☞앞서 제시된 Euler 법의 것과 대응되는 Runge-Kutta법의 프로그램

◎수치계산 결과의 해설

[그림 0A] Euler Method: R = 100, L=2.0e-1, C = 1.0e- 5
X-axis, Y-axis : non-log scales
[프로그램 예1]의 대응 그래프(Euler 법)

[그림 0B] Runge-Kutta Method: R=100, L=2.0e-1, C=1.0e- 5
X-axis, Y-axis : non-log scales
[프로그램 예 1]의 대응 그래프(4차 Runge-Kutta법), 이후 모든 그래프는 Runge-Kutta법에 의해 수치적으로 계산한 결과이다.

[그림 1A] Runge-Kutta Method: L = 1.0e-8, C = 1.0e- 8
X-axis : log scale
X-축은 시간(단위 초)을 나타내고 log scale이다. L=1.0e-8H, C=1.0e-8F로 고정하고, R=10, 20, 50, 100Ω일 때, I(t)와 Q(t) 들의 8가지 그래프를 나 타낸다. 여기서 Q(t)의 그래프에는 실제보다 1.0e7이 곱해져 나타나 있다. 그림에서 보듯이 I(t)는 0.1 μs에서 많이 감소해 있다.

[그림 1B] Runge-Kutta Method: L = 1.0e-8, C = 1.0e- 8
X-axis : non-log scale
[그림 1A]와 같은 조건에서 I(t)와 Q(t)를 나타내는데, 여기서는 X-축이 log scale이 아니다. 그래프에서 보듯이 Q(t)는 지수적으로 증가하고 있음을 알 수 있다.

[그림 2A] Runge-Kutta Method: L = 1.0e-7, C = 1.0e- 7
X-axis : log scale
X-축은 시간을 나타내고 log scale이다. L=1.0e-7H, C=1.0e-7F로 고정하고, R=10, 20, 50, 100Ω일 때, I(t)와 Q(t)들의 8가지 그래프를 나타낸다. 여 기서 Q(t)의 그래프에는 실제보다 1.0e6이 곱해져 나타나 있다.

[그림 2B] Runge-Kutta Method: L = 1.0e-7, C = 1.0e- 7
X-axis : non-log scale
[그림 2A]와 같은 조건에서 I(t)와 Q(t)를 나타내는데, 여기서는 X-축이 log scale이 아니다. 그래프에서 보듯이 Q(t)는 지수적으로 증가하고 있음을 알수 있다.

[그림 3A] Runge-Kutta Method: L = 1.0e-6, C = 1.0e- 6,
X-axis : log scale
X-축은 시간을 나타내고 log scale이다. L=1.0e-6H, C=1.0e-6F로 고정하고, R=10, 20, 50, 100Ω일 때, I(t)와 Q(t)들의 8가지 그래프를 나타낸다. 여 기서 Q(t)의 그래프에는 실제보다 1.0e6이 곱해져 나타나 있다.

[그림 3B] Runge-Kutta Method: L = 1.0e-6, C = 1.0e- 6,
X-axis : non-log scale
[그림 3A]와 같은 조건에서 I(t)와 Q(t)를 나타내는데, 여기서는 X-축이 log scale이 아니다. 그래프에서 보듯이 Q(t)는 지수적으로 증가하고 있음을 알수 있다.

[그림 4A] Runge-Kutta Method: R = 10, L = 1.0e-8
X- axis : log scale
R=10Ω, L=1.0e-8H로 고정하고, C=1.0e-8, 1.0e-7, 1.0e-6F일 때, I(t)와 Q(t)들의 6가지 그래프를 나타낸다. C가 증가할 때 I(t)와 Q(t)도 동시에 증 가함을 알 수 있다.

[그림 4B] Runge-Kutta Method: R = 10, L = 1.0e-8
X- axis : non-log scale
[그림 4A]와 같은 조건에서 I(t)와 Q(t)를 나타내는데, 여기서는 X-축이 log scale이 아니다. 그래프에서 보듯이 Q(t)는 지수적으로 증가하고 있음을 알 수 있다.

[그림 5A] Runge-Kutta Method: R = 10, L = 1.0e-7
X- axis : log scale
R=10Ω, L=1.0e-7H로 고정하고, C=1.0e-8, 1.0e-7, 1.0e-6F일 때, I(t)와 Q(t)들의 6가지 그래프를 나타낸다. C가 증가할 때 I(t)와 Q(t)도 동시에 증 가함을 알 수 있다.

[그림 5B] Runge-Kutta Method: R = 10, L = 1.0e-7
X- axis : non-log scale
[그림 5A]와 같은 조건에서 I(t)와 Q(t)를 나타내는데, 여기서는 X-축이 log scale이 아니다. 그래프에서 보듯이 Q(t)는 지수적으로 증가하고 있음을 알수 있다.
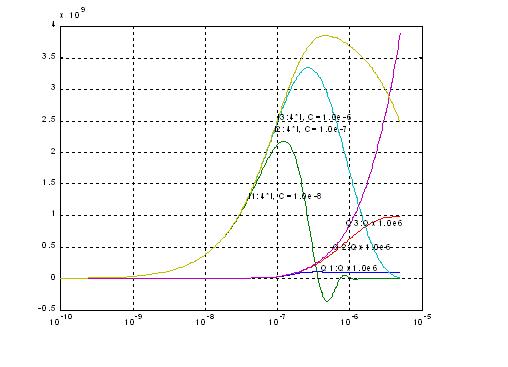
[그림 6A] Runge-Kutta Method: R = 10, L = 1.0e-6
X- axis : log scale
R=10Ω, L=1.0e-6H로 고정하고, C=1.0e-8, 1.0e-7, 1.0e-6F일 때, I(t)와 Q(t)들의 6가지 그래프를 나타낸다. C가 증가할 때 I(t)와 Q(t)도 동시에 증 가함을 알 수 있다.

[그림 6B] Runge-Kutta Method: R = 10, L = 1.0e-6
X- axis : non-log scale
[그림 6A]와 같은 조건에서 I(t)와 Q(t)를 나타내는데, 여기서는 X-축이 log scale이 아니다. 그래프에서 보듯이 Q(t)는 지수적으로 증가하고 있음을 알 수 있다.

[그림 7A] Runge-Kutta Method: R = 20, C = 1.0e-8
X- axis, Y-axis : log scales
R=20Ω, C=1.0e-8F로 고정하고, L=1.0e-8, 1.0e-7, 1.0e-6H일 때, I(t)와 Q(t)들의 6가지 그래프를 나타낸다. L이 증가할 때 Q(t)는 지수적으로 증가 하고 적당한 시간(0.1 μs)에서 그 증가폭이 둔화 된다. 이로 인해 I(t)가 증가후 감소하게 된다.

[그림 7B] Runge-Kutta Method: R = 20, C = 1.0e-8
X- axis: non-log scale, Y-axis: log scale
[그림 7A]와 같은 조건에서 I(t)와 Q(t)를 나타내는데, 여기서는 X-축이 log scale이 아니다. 그래프에서 보듯이 Q(t)는 지수적으로 증가하고 있음을 알수 있다.

[그림 8A] Runge-Kutta Method: R = 20, C = 1.0e-7
X- axis, Y-axis : log scales
R=20Ω, C=1.0e-7F로 고정하고, L=1.0e-8, 1.0e-7, 1.0e-6H일 때, I(t)와 Q(t)들의 6가지 그래프를 나타낸다. L이 증가할 때 Q(t)는 지수적으로 증가 하고 적당한 시간(0.1 μs)에서 그 증가폭이 둔화 된다. 이로 인해 I(t)가 증가후 감소하게 된다. 그러나 여기서는 [그림 7A]보다 복록한 정도가 둔하다.

[그림 8B] Runge-Kutta Method: R = 20, C = 1.0e-7
X- axis: non-log scale, Y-axis: log scale
[그림 7A]와 같은 조건에서 I(t)와 Q(t)를 나타내는데, 여기서는 X-축이 log scale이 아니다.

[그림 9A] Runge-Kutta Method: R = 20, C = 1.0e-6
X- axis, Y-axis : log scales
R=20Ω, C=1.0e-6F로 고정하고, L=1.0e-8, 1.0e-7, 1.0e-6H일 때, I(t)와 Q(t)들의 6가지 그래프를 나타낸다. L이 증가할 때 Q(t)는 지수적으로 증가 하고 적당한 시간(0.1 μs)에서 그 증가폭이 둔화 된다. 이로 인해 I(t)가 증가후 감소하게 된다. 그러나 여기서는 [그림 8A]보다 복록한 정도가 둔하다.

[그림 9B] Runge-Kutta Method: R = 20, C = 1.0e-6
X- axis: non-log scale, Y-axis: log scale
[그림 9A]와 같은 조건에서 I(t)와 Q(t)를 나타내는데, 여기서는 X-축이 log scale이 아니다. 그래프에서 보듯이 Q(t)는 지수적으로 증가하고 있음을 알수 있다.

[그림 10A] Q0*exp[-t/(RC)] : R = 100, 50, 10, C = 1.0e- 8
X-axis : non-log, Y-axis : log scale
C=1.0e-8F로 고정하고, 그래프의 높이에 대응하여, 차례로 R=10, 50, 100Ω일 때 지수함수 Q(t)=Q0exp[-1/(RC)]의 그래프를 나타낸다. Y- 축은 log scale로 나타내고 있다.

[그림 10B] Q0*exp[-t/(RC)] : R = 100, 50, 10, C = 1.0e- 7
X-axis : non-log, Y-axis : log scale
C=1.0e-7F로 고정하고, 그래프의 높이에 대응하여, 차례로 R=10, 50, 100Ω일 때 지수함수 Q(t)=Q0exp[-1/(RC)]의 그래프를 나타낸다. Y- 축은 log scale로 나타내고 있다.
◎수치해석 결과 접지공사 시 RLC 값에 대한 Trend
○R 값은 낮을 수록 방전시간이 빨라진다. L=1×10-8 H, C=1×10-8 F일 경우 R~20 Ω이면 방전시간이 0.15 ㎲이므로(반치폭 기준) 실제로 현장에서도 문제가 없을 것으로 추정된다.
○RLC 값이 크게 되면 예상했던 대로 over-damping oscillation이 일어나게 되므로 장비가 손상될 확률이 높게 된다. L과 C의 의존성을 보기 위하여 R 값을 고정시키고 L과 C의 값을 증가시켰을 때, 회로에 흐르는 전류는 증가하고 방전되는 시간도 증가하게 되어 회로 내의 소자가 손상될 확률이 높아지게 된다.
◎수치해석 결과에 대한 Trend
○R 값은 낮을수록 방전시간( 0.15 ㎲(반치폭 기준))이 빨라지고 L=1×10-8 H, C=1×10-8 F일 경우 R~5 Ω(임피던스)이면, 낙뢰나 서지, Noise, 이상 전압이 발생된다하여도 장비 보호에 문제가 없을 것으로 수치해석 결과가 나온다.
|