A CRITICAL REVIEW OF NONCONVENTIONAL APPROACHES TO LIGHTNING PROTECTION
 A CRITICAL REVIEW OF NONCONVENTIONAL APPROACHES TO LIGHTNING PROTECTION
A CRITICAL REVIEW OF NONCONVENTIONAL APPROACHES TO LIGHTNING PROTECTION
BY M. A. UMAN AND V. A. RAKOV
Neither data nor theory supports claims that “lightning elimination” and “early streamer
emission” techniques are superior to conventional lightning protection systems
CONVENTIONAL SYSTEM
Properly designed conventional lightning protection systems for ground-based structures serve to provide lightning attachment points and paths for the lightning current to follow from the attachment points into the ground without harm to the protected structure. Such systems are basically composed of three elements: 1) “air terminals” at appropriate points on the structure to intercept the lightning, 2) “down conductors”to carry the lightning current from the air terminals toward the ground, and 3) “grounding electrodes”to pass the lightning current into the earth. The three system components must be electrically well connected. Many national and international standards describe conventional lightning protection systems (e.g., NFPA 1997, hereafter NFPA 780), and the efficacy of the conventional approach has been well demonstrated in practice (e.g., Harris 1843, 140-156; Symons 1882; Lodge 1892; Peters 1915; Covert 1930; Keller 1939; Szpor 1959). The classic text on the conventional lightning protection of structures is Golde (1973). The theoretical justification of the conventional approach is fairly crude, in part due to our incomplete understanding of lightning’s attachment to ground-based objects. Hence, the fact that conventional systems have a history of success in preventing or minimizing damage to structures is the primary justification for their use. It is nevertheless instructive to review the current understanding of the lightning processes, this understanding being consistent with the experience gained from the use of conventional structural lightning protection systems.
The lightning stepped leader, the process that initiates a cloud-to-ground flash, begins in the cloud charge region (near 5-km height in temperate summer for the typical flash that lowers negative charge) and propagates toward Earth at a typical average speed of 105 m s-1. The charge on the leader channel (effectively drained from the cloud charge source) produces an electric field near the earth’s surface that is enhanced by objects projecting above the surface such as trees and grounded air terminals on struc-tures. When the leader is tens to hundreds of meters above ground, this electric field becomes large enough to produce electrical breakdown between the leader tip and the ground or between the leader tip and one
of the elevated objects. Such electrical breakdown, which occurs in long laboratory sparks at an average gap electric field of a few hundred kilovolts per meter (e.g., Chowdhuri 1996, 226-240; Bazelyan and Raizer 2000), involves one or more upward-connecting leaders emanating from the ground or from grounded objects. One of these upward-connecting leaders meets one of the branches of the downward-propagating leader and establishes a conducting path between cloud and ground. Figure 1 shows a simplified picture of lightning attachment to a structure that is protected by a conventional lightning protection system employing air terminals in the form of lightning rods.
We now review the engineering models involved in the conventional approach to lightning protection. The attachment of the leader to the struck object is often described using the so-called electrogeometrical theory, the core of which is the concept of a “striking distance.” This concept obscures some of the significant physics but allows the development of relatively simple and useful techniques for designing conventional lightning protection systems. The striking distance is defined as the distance from the tip of the leader to the object to be struck at the instant that the breakdown electric field is reached across the final gap or, alternatively, is defined as the distance from the leader tip to the object to be struck at the time when an upward-connecting leader is initiated from the object to be struck. Given an assumed striking distance, one can define an imaginary surface above the ground and above objects on the ground such that, when the downward-propagating leader passes through that surface at a specific location, the leader is “captured” by a specific point on the ground or on a grounded object. The geometrical construction of this surface can be accomplished simply by rolling an imaginary sphere of radius equal to the assumed striking distance across the ground and across objects on

FIG. 1. The lightning attachment process: (a) the stepped leader descends to within about 100 m of a house with conventional lightning protection (not to scale), (b) upward leaders launched from lightning rods and nearby tree, and (c) connection made between one branch of the downward-moving stepped leader and one upward-moving leader determining the path for current flow of the resulting upward-propagating return stroke.
the ground, the so-called rolling sphere method (e.g., Lee 1978; NFPA 780). The locus of all points traversed by the center of the rolling sphere forms the imaginary capture surface referred to above. Those points that the rolling sphere touches can be struck, according to this approach; and points where the sphere does not touch cannot be. Figure 2 illustrates the rolling sphere approach. In this approach, any objects beneath the surface shown by the dashed lines in Fig. 2 cannot be struck (are protected), and any groundbased objects projecting through that surface can be struck (are unprotected). In the commonly used rolling sphere approach, the striking distance is assumed to be the same for any object projecting above the earth’s surface or for the earth itself. There are variations of this technique in which the assumption of equal striking distances for different objects and for the earth is replaced by the assumption of different striking distances for objects of different geometry (e.g., Eriksson 1987a,b). One can use the rolling sphere method with constant assumed sphere radius to position air terminals on a structure so that one of the terminals, rather than a roof edge or other part of the structure, initiates the upward leader that connects to the downward leader; that is, the striking distance to an air terminal is reached by a downward-propagating leader before the striking distance to a portion of the protected structure is reached.
Assuming a distribution of charge along the leader channel and a value of breakdown field, one can relate the striking distance to the charge on the stepped leader channel and then using the observed correlation between the charge and peak current of the resultant return stroke (Berger et al. 1975) one can find the relationship between the striking distance and the return stroke peak current. Given all the assumptions involved, this relationship is necessarily crude. According to International Standard IEC 61024-1 (IEC 1993) 99% of striking distances exceed 20 m, 20 m being associated with a first stroke peak current of about 3 kA; 91% exceed 45 m, associated with about 10 kA; and 84% exceed 60 m, associated with about 16 kA. Clearly, these are very rough estimates. The typical first stroke peak current is near 30 kA (Berger et al. 1975) for which various calculated striking distances, using different assumptions on breakdown parameters, are generally between 50 and 150 m (Golde 1977), consistent with the typical observed striking distances reviewed by Uman (1987, 99-109, 205-230). For the placement of air terminals in a conventional lightning protection system, NFPA 780 recommends adopting a striking distance of 46 m. Smaller assumed striking distances result in a more
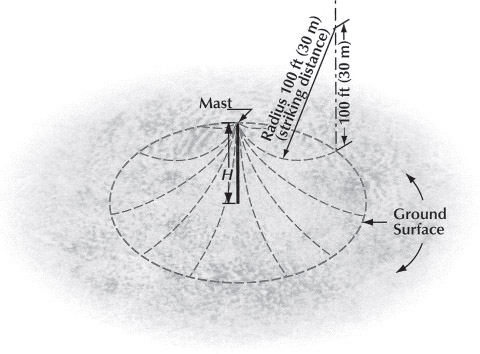
FIG. 2. Zone of protection for a single mast of height H, as determined by the rolling sphere method.
Adapted from NFPA 780.
conservative approach to protection; that is, more air terminals are required, as can be inferred from Fig. 2, and lightning discharges with lower peak currents are intercepted by the air terminals. According to some standards, a wire mesh covering the top of the structure may play the role of the air terminals. (Note that the rolling sphere method would predict that lightning can attach to the structure between the metal mesh conductors unless the mesh is elevated above the top of the structure.) For example, IEC (1993) states that a mesh size of 15 m × 15 m is equivalent to protection with lightning rod air terminals designed for an assumed 45-m striking distance. Apparently, the specified relationship between mesh size and striking distance is a matter of experience rather than theory.
NONCONVENTIONAL SYSTEMS
With this brief background in conventional lightning protection, we now, and in the following sections, consider nonconventional approaches to lightning protection. Nonconventional lightning protection schemes for ground-based structures generally fall into one of two classes: 1) “lightning elimination” or 2) “early streamer emission.” Nonconventional systems using these two techniques are commercially available under a variety of trade names and are claimed to be superior to the conventional lightning protection described above. The primary intent of this paper is to review the literature on the two nonconventional approaches in conjunction with the pertinent lightning literature so that we can examine the hypothesis that systems employing these techniques function as advertised, that is, are superior to the conventional technique described in the section “Conventional Systems.” We will show that the suggested advantages of the nonconventional methods over the conventional technique are not supported by the available experimental data or by theory. This conclusion is consistent with that of Golde (1977) who reviewed the nonconventional approaches to lightning protection based on the information available at the time of his writing.
LIGHTNING ELIMINATION
General information and theory. The primary claim of the proponents of lightning elimination systems (which more recently have been called “charge transfer systems”) is that those systems produce conditions under which lightning either does not occur or cannot strike the protected structure, as opposed to the conventional approach of intercepting the imminent lightning strike and rendering it harmless by providing a nondestructive path for the lightning current to flow to ground. Lightning elimination systems include one or more elevated arrays of sharp points, often similar to barbed wire, that are installed on or near the structure to be protected. These arrays are connected to grounding electrodes via down conductors as in the case of conventional lightning protection systems. The principle of operation of lightning elimination systems, according to their proponents, is generally that the charge released via corona discharge at the sharp points will either (i) discharge the overhead thundercloud, thereby eliminating any possibility of lightning (this is why such arrays are sometimes referred to as “dissipation arrays”) or (ii) discourage a downward-moving leader from attaching to the array and to the structure to be protected by reducing the electric field near the array and, hence, suppress the initiation of an upward-connecting leader.
According to Muller-Hillebrand (1962a) and Golde (1977), the idea of using multiple-point corona discharge to “silently” discharge thunderclouds and thus to prevent lightning was first proposed in 1754 by Czech scientist Prokop Divisch, who constructed a “machina meteorologica” with over 200 sharp points installed on a 7.4-mhigh wooden framework; although as early as 1751 Benjamin Franklin, based on his small-scale laboratory experiments, had suggested that “the wonderful effects of pointed bodies” might reduce or eliminate the deleterious
effects of lightning (Cohen 1990). Hughes (1977) states that a patent for a multiple-point system was issued in 1930 to J. M. Cage of Los Angeles, California. The patent describes the use of point-bearing wires suspended from a steel tower to protect petroleum storage tanks from lightning. A similar system, commonly referred to as a dissipation array system (DAS) or a charge transfer system (CTS), has been commercially available since 1971 although the product name and the name of the company that marketed it have changed over time (Carpenter 1977; Carpenter and Auer 1995). Most lightning elimination systems were originally designed for tall communication towers, but recently they have been applied to a wide range of systems and facilities including electrical substations, power lines, and airports.
Carpenter and Auer (1995) give their view of the operation of the dissipation array marketed by the leading manufacturer. This array, schematically shown in Fig. 3, consists of 1) an “ionizer” with many hundreds of points, 2) a “ground current (or charge) collector,” which is essentially a grounding system, and 3) conductors (labeled “service wires” in Fig. 3) connecting the ionizer to the grounding system. The ground charge collector is said to “neutralize” the positive charge on the ground that would otherwise accompany the negative cloud charge overhead. It is further stated that “millions of ionized air molecules” from the ionizer are drawn away from the site (presumably related to the positive charge “neutralized”
on the ground) toward the thundercloud by the high electrostatic field, and, in the process, “a protective ‘space charge’ or ion cloud is formed between the site
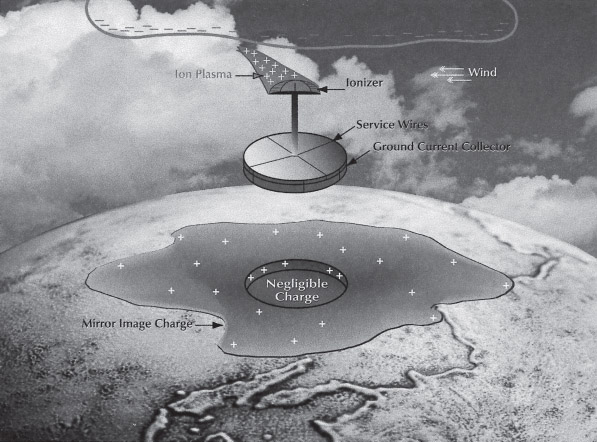
FIG. 3. Diagram of a DAS. Adapted from Carpenter and Auer (1995).
and the storm.” According to Carpenter and Auer (1995), “many consider the space charge the primary protective mode, saying its function is much like a Faraday shield providing a second mode of protection.” Carpenter and Auer (1995) do not support their description of the principle of operation of dissipation arrays with quantitative arguments. In a comment accompanying the paper of Carpenter and Auer (1995), Zipse (see also Zipse 1994) points out that trees and blades of grass generate corona discharge, often exceeding that of dissipation arrays, without apparently inhibiting lightning. This same point has been previously made by Zeleny (1934) and by Golde (1977). Zeleny (1934) observed that “during a storm in Switzerland the top of a whole forest was seen to take on a vivid glow, repeatedly, which increased in brilliance until a lightning bolt struck.” Ette and Utah (1973) reported that the average corona currents from a metal point and from palm trees of comparable height were similar (see below). Interestingly, Zipse (2001) has referred to the conclusions of Zipse (1994) as “erroneous,” stating that corona on trees is incapable of producing as much charge as the charge transfer system. Zipse (2001) also states that the lightning elimination system may fail to eliminate lightning, and, in this case, it acts as a conventional lightning protection system.
We now estimate the value of corona-produced charge and the distance over which such charge can move during the typical cloud-charge regeneration time, of the order of 10 s (e.g., Chauzy and Soula 1987), between lightning discharges. In the absence of a downward-propagating leader, both the charged light ions and the heavier aerosol ions formed by ionparticle attachment in the humid air near the points of a dissipation array move in response to 1) the electric field of the cloud charge, other space charge, and the charge on the ground and on grounded objects; and 2) the wind. Typical electric fields near the ground under thunderstorms seldom exceed 10 kV m-1, while 100 m or so above the ground the fields can be near 50 kV m-1 (Chauzy et al. 1991; Soula and Chauzy 1991). The mobilities of atmospheric light ions in electric fields of 10 to 50 kV m-1 are in the range of 1 to 3 × 10-4 m2 V-1 s-1 (Chauzy and Rennela 1985; Chauzy and Soula 1999). Heavier ions move two orders of magnitude more slowly. Thus, above the field enhancement region of the dissipation array, upward-directed drift velocities of light ions may approach 15 m s-1. Horizontal wind speeds of several meters per second are common under thunderclouds so that the light ions formed by corona discharge will also move horizontally. If sufficient charge is emitted from a dissipation array, there will be a reduction of the local electric field near the array and an enhancement of the field at a distance from the array of the order of the size of the array, the magnitude of this effect depending on the magnitudes of the corona current and the wind. The corona current is self-limiting in the sense that the corona-produced charge shields the array and therefore reduces the electric field that drives the corona discharge. The negative cloud charge that is the source of most cloud-to-ground lightning is located at 5 km or so in temperate regions and has a value of some tens of coulombs. During the 10 s of cloud-charge regeneration, charges emitted by the array may move a vertical distance of up to 150 m and, if there is, for example, a 5 m s-1 horizontal wind, horizontally about 50 m. A vertical wind would also have an effect (Chalmers 1967, 239-262). As the ions move away from the array, their shielding effect is reduced, and the electric field near the array may increase. The effect of corona on upward-lightning leader initiation in a slowly varying thundercloud electric field has been theoretically studied by Aleksandrov et al. (2001). However, they did not consider the practically important (from the lightning protection point of view) case of the initiation of an upward-connecting leader in response to the approaching downward leader. If the rapidly varying electric field associated with the approaching stepped leader acts to overcome the shielding effect of corona space charge near the grounded object, the resultant upward-connecting leader will escape the space charge cloud and intercept the descending leader, as discussed in the section “Conventional systems.”
According to the Draft Standard regarding charge transfer systems submitted to the IEEE (IEEE P1576/ D2.01 2001) by their proponents, a 12-point array will produce a corona current of 700 μA under a thunderstorm. Zipse (2001) reported on a corona current of 500 μA from four sets of three points installed on a 20-m pole, apparently measured in the absence of lightning in the immediate vicinity of the pole. It is not clear who performed these measurements or how. More important, it is not clear if the reported value is average or peak current. The actual corona current from a large number of points depends on the spacing between the points since the corona from each point reduces the electric field at adjacent points and hence their individual current output (e.g., Chalmers 1967, 239-262). Thus, many closely spaced points do not necessarily emit more corona current than several well-separated points. Ette and Utah (1973), in perhaps the best study to date of corona current from grounded objects under thunderstorms, found the average corona current from a 10-m metal point to be about 0.5 μA, while palm trees of 13- and 18-m height produced between 1 and 2 μA. IEEE P1576/ D2.01 (2001) states that the appropriate array design should consist of a sufficient number of corona points so that the array will emit a charge equal to that on a stepped leader, apparently taken as 5 C, in a time of 10 s, the cloud-charge regeneration time noted in the previous paragraph. If, for example, a current of roughly l mA were emitted from a 10-point array, as stated in IEEE P1576/D2.0 (2001) without adequate experimental evidence, then a charge of 10-2 C would flow into the air in the 10-s charge regeneration time. To emit 5 C to the air in 10 s, the array would require 5000 well-separated points. According to Zipse (2001), a typical array contains 4000 points, although usually located in close proximity to each other. There are no well-documented data in the literature on corona current that could be extrapolated to a large array and certainly no evidence that several coulombs of corona charge can be released in 10 s or so from an array of any practical dimensions.
Golde (1977) has suggested that dissipation arrays installed on tall structures, typically towers, will inhibit upward lightning flashes (initiated by leaders that propagate upward from the tall structure into the cloud) by modifying the needlelike shape of the structure tops to a shape that has a less pronounced fieldenhancing effect. While this suggestion is not unreasonable, there are no measurements to support it. Upward lightning discharges occur from objects greater than 100 m or so in height (above flat terrain) and most lightning associated with objects of height above 300 m or so is upward (Eriksson 1978; Rakov and Lutz 1988). In this view, dissipation arrays would inadvertently reduce the probability of occurrence of these upward flashes, which represent the majority of flashes to very tall towers. The upward flashes contain initial continuous current and often contain subsequent strokes similar to those in normal cloud-toground lightning (e.g., Uman 1987; Rakov 2001), thus having the potential for damage to electronics. It is important to note that damage to electronics can be prevented or minimized by the use of so-called surge protection, as opposed to the structural protection that is the subject of this paper. The reduction of the electric field at the tower top due to the increase of its effective radius of curvature, discussed above, does not require either the release of space charge to provide shielding or the dissipation of cloud charge. The view of Golde (1977) has been expanded on by Mousa (1998), who argues that the suppression of upward flashes will be particularly effective for towers of 300-m height or more and that dissipation arrays will have no effect whatsoever on the frequency of strikes to smaller structures such as power substations and transmission line towers.
Mousa (1998) has reviewed lightning elimination devices that are claimed to employ corona discharge from multiple points. Mousa (1998) shows drawings of six so-called dissipaters produced by five different manufacturers. One of these, the umbrella dissipater, has been described by Bent and Llewellyn (1977) as about 300 m of barbed wire wrapped spirally around the frame of a 6-m-diameter umbrella. The barbed wire has 2-cm barbs with four barbs separated by 90° placed every 7 cm along the wire. The umbrella dissipater described by Bent and Llewellyn (1977) was mounted on a 30.5-m tower in Merritt Island, Florida. Mousa (1998) also describes a ball dissipater, a barbed power line shield wire, a conical barbed wire array, a cylindrical dissipater, a panel dissipater (fakir’s bed of nails), and a doughnut dissipater. Mousa (1998) also discusses the extensive grounding procedures used by the manufacturers and installers of lightning elimination devices (see also Zipse 2001). The leading manufacturer (see Carpenter and Auer 1995) typically uses a buried ground ring (the ground current collector in Fig. 3) that encircles the structure with 1-m-long ground rods located at 10-m intervals around the ring. In poorly conducting soil, the same manufacturer uses chemical ground rods of its own design, hollow copper tubes filled with a chemical that leaches into the soil in order to reduce the soil conductivity surrounding the grounding system. In addition to the structural lightning protection, this same manufacturer highly recommends the installation of surge protective devices on sensitive electronics at the same time that the dissipation array system is installed. Carpenter (1977) lists many customers who report a cessation of lightning-caused damage after installation of the system he manufactures (presumably including both structural and surge protection components). However, as Mousa (1998) points out, most lightning elimination systems can, in principle, provide conventional lightning protection (see also Zipse 2001); that is, they can intercept a lightning strike and direct its current into the ground without damage to themselves or to the protected structure if there is sufficient coverage of the structure by arrays (air terminals). Further, damage to electronics within the structure can be eliminated or minimized by way of the installation of surge protective devices and good grounding, this protective effect having nothing to do with the structural protection (lightning elimination) component.
Observations. We summarize now the records of observed lightning strikes to dissipation arrays. In 1988 and 1989 the Federal Aviation Administration (FAA) conducted studies of the performance of dissipation arrays relative to conventional lightning protection systems at three Florida airports (FAA 1990). An umbrella dissipation array installed on the central tower of the Tampa International Airport was struck by lightning on 27 August 1989, as shown by video and current records (FAA 1990, see appendix E). Carpenter and Auer (1995) have disputed the findings of FAA (1990), and Mousa (1998) has reviewed the attempts of the dissipation array manufacturer to suppress FAA (1990). Additional lightning strikes to dissipation arrays are described by Durrett (1977), Bent and Llewellyn (1977), and Rourke (1994). The former two references describe strikes to towers protected by dissipation arrays at the Kennedy Space Center, Florida, and at Eglin Air Force Base, Florida, respectively. Rourke (1994) considers lightning strikes to a nuclear power plant. The plant was struck by lightning three times in two years, 1988 and 1989, before having dissipation arrays installed. After dissipation array installation, the plant was also struck three times in two years, 1991 and 1992. Rourke (1994) notes that “there has been no evidence that lightning dissipation arrays can protect a structure by dissipating electric charge prior to the creation of the lightning.”
Kuwabara et al. (1998) reported on a study of dissipation array systems that were installed in summer 1994 atop two communication towers on the roof of a building in Japan. Kuwabara et al. (1998) state that the dissipation array “was not installed per the manufacturer’s recommendations as a result of the building construction conditions in Japan.” Measurements of lightning current waveforms during strikes to the towers were made prior to the installation of dissipation arrays, from winter 1991 to winter 1994, and after the installation, from winter 1995 to winter 1996. Additionally, six direct strikes to the towers with the arrays installed were photographed between December 1997 and January 1998. Twenty-six lightning current waveforms were recorded in the three years before installation of the dissipation arrays and 16 in the year or so after installation. The statistical distribution of peak currents was essentially the same before and after installation. Estimated peak currents varied from 1 to 100 kA. Kuwabara et al. (1998) state that after installing the dissipation arrays, improving the grounding, and improving the surge protection in summer 1994 “malfunctions of the telecommunications system caused by lightning direct strike have not occurred,” whereas they were common before. Apparently, the presence of the dissipation arrays neither prevented the lightning strikes nor changed the characteristics of the lightning stroke current, while the equipment damage was eliminated by means of improved surge protection and grounding.
EARLY STREAMER EMISSION
General information and theory. The attractive effect of an air terminal would be enhanced by a longer upward-connecting leader (e.g., Rakov and Lutz 1990); the longer the
leader, the greater the enhancement. Early streamer emission (ESE) systems are similar to conventional structural lightning protection systems except that they employ air terminals that, according to their proponents, launch an upward-connecting leader to meet the descending-stepped leader at an earlier time than would a conventional air terminal having similar geometry and installed at the same height. This earlier initiated upward-connecting leader is claimed to be capable of extending to significantly longer distances and, as a result, to provide a significantly larger zone of protection than the upward-connecting leader from a conventional air terminal of the same height. If this be true, it would follow that a single early streamer emission air terminal could replace many conventional air terminals, which is the primary claim of ESE proponents. Without this claim, ESE systems would be indistinguishable from conventional systems.
There are several types of early streamer emission systems. All employ specially designed air terminals that are claimed to create enhanced ionization near the air terminal, either by employing radioactive sources, by a special arrangement of passive electronics and electrodes that facilitate the electrical breakdown of small spark gaps in a high electric field of the approaching stepped leader, or by the application of an external voltage to the air terminal from a manmade source. The first early streamer emission devices were so-called radioactive rods, rods with radioactive material placed on them, although when these were initially marketed the term early streamer emission had not been coined. According to Baatz (1972), in 1914 the Hungarian physicist L. Szillard first raised the question of whether the attractive effect of a lightning rod could be increased by the addition of a radioactive source.
Various tests in the field and the laboratory have shown that, under thunderstorm conditions, there is little or no difference between the action of a radioactive rod and that of a similarly installed conventional rod of the same height (e.g., Muller-Hillebrand 1962b; Baatz 1972). Heary et al. (1989) published laboratory tests purporting to show the superiority of radioactive rods over conventional rods, but, in discussions accompanying that paper, five researchers (G. Carraca, I. S. Grant, A. C. Liew, C. Menemenlis, and A. M. Mousa) use the paper’s results to argue otherwise. Mackerras et al. (1987) have given examples of the failure of radioactive lightning protective systems in Singapore where, at the time of their study, over 100 such systems were installed. Golde (1977) cites the failure of a radioactive lightning rod to prevent lightning from knocking the papal crest off Bernini Colonnade at the Vatican on 6 March 1976. The crest was located about 150 m from a 22-m-high radioactive rod that was supposed to protect it.
Surveys of the ESE literature by van Brunt et al. (1995; see also van Brunt et al. 2000) and Bryan et al. (1999), commissioned by the U.S. National Fire Protection Association, were part of an independent investigation to determine if there should be a U.S. national standard for early streamer emission systems such as the NFPA 780 for conventional systems. Based on these surveys, NFPA concluded that there was “no basis for the claims of enhanced protection” of ESE systems relative to conventional systems and, hence, no basis for issuing a standard for ESE systems. Nevertheless, there are presently both a French Standard (1995) and a Spanish Standard (1996) for the laboratory qualification of early streamer emission
systems for lightning protection of structures. Strong arguments can be made that no laboratory spark test can be extrapolated to describe the case of natural lightning. For example, the length of individual steps in the lightning stepped leader is of the order of tens of meters, a distance considerably larger than the length of laboratory spark gaps, of the order of a meter, specified to test and certify ESE systems [e.g., French Standard (1995) that requires a gap no smaller than 2 m with the air terminal being between 0.25 and 0.5 times the gap size]. It is not likely that one can adequately simulate the natural-lightning attachment process in a 2-m laboratory gap. As another example, in natural lightning the downward negative leader from the cloud has a length of many kilometers while the positive upward-connecting discharge from the ground or from elevated objects is generally much shorter, some tens to hundreds of
meters long. On the other hand, in laboratory spark studies intended to simulate lightning strikes to grounded objects, positive leaders are always much longer than negative leaders.
ESE proponents argue that ESE air terminals emit a positive upward-moving connecting leader (intended to meet the downward-moving negative stepped leader that initiates the usual cloud-to-ground lightning flash) at an earlier time, by a time interval Δt, than do conventional air terminals. They claim that this earlier initiated leader occurs in a smaller
electric field than is required for the initiation of a leader by a conventional rod. Further, they translate the claimed time advantage Δt into a length advantage, ΔL, for the earlier initiated leader via ΔL = vΔt, where v is the speed of the upward-connecting leader. ESE proponents assume that the speed of the upwardconnecting leader is of the order of 106 m s-1 (e.g., French Standard 1995). This value of leader speed is arbitrary, since it is not supported by experimental data, as discussed next. The only existing measurements
of upward positive leader speeds in natural lightning are due to McEachron (1939), Berger and Vogelsanger (1966, 1969), and Yokoyama et al. (1990). McEachron (1939) reported that upward positive leaders initiated from the Empire State Building propagated at speeds ranging from 5.2 × 104 to 6.4 ×105 m s-1, with the lengths of individual leader steps ranging from 6.2 to 23 m. Berger and Vogelsanger (1966, 1969) measured speeds between 4 × 104 and about 106 m s-1 for seven upward positive leaders, with the individual leader step lengths ranging from 4 to 40 m. Further, for four of the seven leaders Berger and Vogelsanger (1966) measured speeds ranging from 4 to 7.5 × 104 m s-1 and step lengths from 4 to 8 m at altitudes ranging from 40 to 110 m from the tower top, where a connection between a downward leader and an upward-connecting leader would be expected. Yokoyama et al. (1990) measured, for three cases, upward leader speeds between 0.8 to 2.7 × 105 m s-1. They show figures in which the stepping of both the upward and downward leader is apparent. Yokoyama et al. (1990) report that the lengths of the upwardconnecting leaders whose speeds they measured were from some tens of meters to over 100 m at the time that a connection was made with the downward-moving stepped leader. Their measurements are apparently the only ones of the speeds of upward-connecting leaders that actually connect to downward leaders below the cloud base, as opposed to upward positive leaders in upward flashes that enter the cloud. Interestingly, positive upward-connecting leaders in laboratory spark experiments typically have speeds of 104 m s-1, an order of magnitude lower than typical values in natural lightning and two orders of magnitude lower than the 106 m s-1 assumed by ESE proponents (e.g., Berger 1992). Yokoyama et al. (1990) also reported on the speed of individual optical step formation, this irrelevant measurement being sometimes referenced by ESE proponents in support of the ar Mackerras et al. (1997) and Chalmers et al. (1999) critically review the proposed ESE techniques. Both papers raise the important question of whether an upward-connecting leader, if indeed launched by an ESE rod earlier than for a conventional rod, and hence launched in a lower electric field, is able to propagate in the required manner in this lower field. According to Mackerras et al. (1997), once the upward-connecting leader propagates into the space remote from the air terminal, its farther progression depends upon the supply of energy from the electric field in the space
near the tip of the leader and upon the dielectric properties of the air undergoing breakdown, neither of these factors being influenced by the air terminal. Using this and geometrical arguments, Mackerras et al. (1997) conclude that “it is not possible to gain a significant improvement in lightning interception performance by causing the early emission of a streamer from an air terminal."
It is necessary for proponents of ESE devices to assume the arbitrary value of v = 106 m s-1 for a value of Δt of about 100 μs in order to claim a significant length advantage ΔL of 100 m for the upward-connecting leader from an ESE rod over that from a conventional rod. If the value of v = 105 m s-1, which is consistent with the available experimental data were used instead, even allowing a 100-μs time advantage and even assuming that the leader could propagate in the lower field in which its initiation is claimed to occur, the length advantage would be only ΔL = 10 m, which is not likely to be significant in most practical situations.
Observations. Two triggered-lightning tests of a commercial ESE system described by Eybert-Berard et al. (1998) are sometimes cited in support of the efficacy of the ESE technique. That particular ESE system had several spark gaps at the tip of the air terminal that were intended to be activated in a sufficiently high electric field. The first triggered-lightning test, conducted in Florida, showed a current pulse of about 0.8-A peak and 2-μs duration from an ESE rod 85 μs prior to a triggered-lightning return stroke to ground
at a distance not given by Eybert-Berard et al. (1998). The ESE rod was not struck. No appreciable current followed the initial pulse in the ESE rod, which suggests that the observed current pulse was not associated with the initiation of an upward leader. Thus, this experiment proves nothing relative to ESE system validation. The second triggered-lightning experiment, conducted in France and described in the same paper, involved lightning that was triggered near an ESE rod with a conventional rod located farther away. The ESE rod was the attachment point of a leader/ return stroke sequence, possibly because it was placed closer to the rocket launcher than the conventional rod. Unfortunately, the positions of the ESE and conventional
rods were not interchanged to see if only the rod (whether ESE or conventional) that is closer to the rocket launcher is always struck or if a more distant ESE rod could compete with a conventional rod placed closer to the launcher.
Thus, there is, in fact, no support for the proposed ESE technique in the results of any experimental study involving either triggered or natural lightning. On the contrary, natural-lightning studies have shown that ESE systems do not work as their proponents claim. Moore et al. (2000a,b) report no advantage of ESE rods over conventional rods from their studies on a mountain top in New Mexico. In fact, they found that in 7 yr of observations neither ESE rods nor sharp conventional rods were struck, while 12 conventional rods with blunt tips (diameters ranging from 12.7 to 25.4 mm) were struck. Case studies in Malaysia by Hartono and Robiah (1995, 1999, manuscript submitted to the NFPA, hereafter HR99; Hartono and
Robiah 2000) show that there was lightning damage to buildings within the advertised protection zone of the ESE systems. These papers include before and after photographs for over two dozen cases, providing direct evidence of the failure of such systems. Interestingly, the studies by Hartono and Robiah (1995) on buildings protected using conventional systems show similar lightning damage. Hartono and Robiah (1995, 2000; HR99) conclude that there is no advantage in using an ESE system relative to conventional systems We do not discuss here the results of laboratory studies of the ESE technique since we do not believe that laboratory sparks can adequately simulate the natural-lightning attachment process, as discussed in the section “General information and theory.”
SUMMARY
The conventional lightning protection technique has proven its effectiveness as evidenced by the comparative statistics of lightning damage to protected and unprotected structures. The rolling sphere method commonly used in the design of such systems is relatively crude, in part, because of our insufficient understanding of the lightning attachment process, but it does represent a useful engineering tool for determining the number and positions of air terminals.
Lightning elimination systems cannot prevent the initiation of lightning in the thundercloud and are unlikely to be able to avert an imminent lightning strike. Further, these systems are indeed struck by lightning, in which case they act as conventional lightning protection systems. The overall lightning elimination system often includes both structural and surge protection components, the latter being likely responsible for the reported improved lightning performance of the protected object.
There is no experimental evidence that an ESE air terminal can protect a larger volume of space (i.e., can attract a lightning to itself from farther away) than can a similarly placed and grounded conventional rod of the same height. An upward-connecting leader speed of 106 m s-1 is required to produce the “length advantage” of 100 m claimed by the proponents of ESE systems in order to demonstrate the superiority of the ESE technique over the conventional method of lightning protection. The typical measured upward positive leader speed is an order of magnitude lower, 105 m s-1, inconsistent with this claim. Given the lack of evidence of the superiority of ESE systems over conventional systems, adequate lightning protection would require that each of them have a similar number of air terminals.
ACKNOWLEDGMENTS
This research was supported in part by NSF Grant ATM-0003994. The authors wish to thank E. P. Krider and an anonymous reviewer for many valuable comments that helped improve the manuscript.